📝 题目描述

题目链接：接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：

1
2
3
4
5
6
7
8
9
10
11
12

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

  • n == height.length
  • 1 <= n <= 2 * 10^4
  • 0 <= height[i] <= 10^5

💡 解题思路

方法一：动态规划

我们先考虑一般情况，特殊情况我们最后再考虑。

①一般情况：

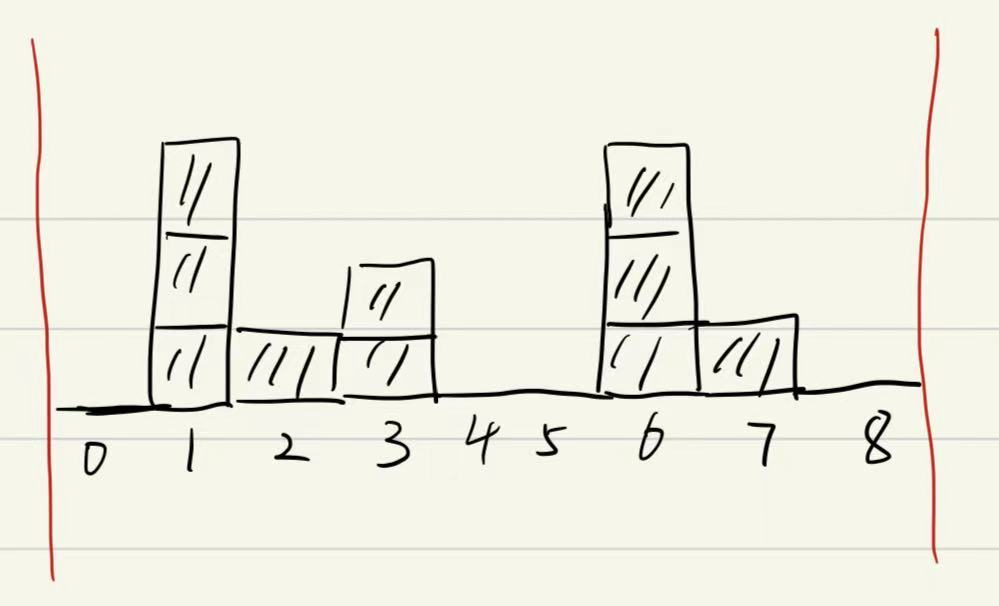
比如，对于上图中的横坐标为2的位置，它在垂直方向能接多少雨水呢？
我们可以得到对于每个横坐标位置，接雨水的量 = 该位置雨水可以淹没多高 - 该位置的高度;
很明显该位置的高度就是height[2] = 1，那么怎么算该位置可以雨水可以淹没多高呢？
这有点像“LeetCode5 - 盛最多水的容器”，比如对于横坐标为2的位置，我们向左看，最高的柱子是横坐标为1的位置（设为leftMax[2] = height[1] = 3），向右看，最高的柱子是横坐标为6的位置（设为rightMax[2] = height[6] = 3）；
这样一来，横坐标为2的位置雨水就能淹没min(leftMax[2],rightMax[2])也就是3的高度了。
可以得出横坐标为2的位置接雨水的量 = 3 - 1 = 2。

②特殊情况：

特殊情况其实也没什么特殊的，就是边界处，对于上图横坐标为0的位置，它再向左没有柱子了，那么我们可以设leftMax[0]=height[0]，同样我们可以设rightMax[8]=height[8]。

规范一些，定义：leftMax[i] 表示下标 i 及其左边的位置中，height 的最大高度（就是同时也看自身的高度）；同理，rightMax[i] 表示下标 i 及其右边的位置中，height 的最大高度。

通过上面的分析，暴力解法呼之欲出了，也就是我们遍历每一个高度，计算它能接到的垂直方向雨水量，然后累加起来。这样的话，对于每个高度我们都要遍历一次整个数组来找到leftMax[i],rightMax[i]，复杂度达到了 O(N2)O(N^2) 。

思考一下，我们发现，其实上面的过程做了很多重复的工作，能不能提前扫描数组，将leftMax[i],rightMax[i]预置好呢？

假设我们要填leftMax数组，也就是“下标 i 及其左边的位置中，height 的最大高度”，想一想，对于位置0，那么leftMax[0] = height[0]没得选；对于位置1，我们也不必重新遍历1前面的数了，直接对比leftMax[0]和height[1]，谁大leftMax[1]就是谁。

也就是说，我们从左往右填leftMax数组，那么leftMax[i]=max(leftMax[i−1],height[i])；

同样，假设我们要填rightMax数组，也就是“下标 i 及其右边的位置中，height 的最大高度”，对于位置n-1，那么rightMax[n-1] = height[n-1]；对于其他位置i，对比rightMax[0]和height[i]，谁大rightMax[k]就是谁。

可以得出，我们从右往左填rightMax数组，rightMax[i]=max(rightMax[i+1],height[i])。

做完这些，那么剩下的只需要从头遍历一下height数组，然后得到min(leftMax[i],rightMax[i])，再减去height[i]，累加一下啊，就得到了正确答案。

方法二：单调栈

我们维护一个单调栈，单调栈存储的是下标，满足从栈底到栈顶的下标对应的数组 height 中的元素递减，并从左往右遍历height[i]：

  1. 如果栈为空，直接进栈；否则判断栈顶元素top对应的height[top]与height[i]的关系：
    • 如果height[top] > height[i]：我们可以想象，栈中的元素对应的height 单调递减，那么直到 height[i] 都是递减的，无法形成低洼接到雨水，于是将 i 进栈；
    • 如果height[top] < height[i]：
      • 如果栈内只有一个元素，那么height[top]前的元素一定因为比height[top]还要低才不在栈中，无法形成低洼，因此直接将 top 出栈，将 i 进栈。
      • 如果栈内至少有两个元素，记 top 的下面一个元素是 left，则由单调性可知 height[left] > height[top] < height[i]， 可以形成一个接雨水的区域，该区域的宽度是 i − left − 1，高度是 min(height[left], height[i]) − height[top] ，为了得到 left，需要将 top 出栈。在对 top 计算能接的雨水量之后，left 变成新的 top。
        2、重复上述操作。

方法三：双指针

想一下刚才的动态规划，需要维护两个数组 leftMax 和 rightMax，因此空间复杂度是 O(N)。是否可以将空间复杂度降到 O(1)?

注意到下标 i 处能接的雨水量由 leftMax[i] 和 rightMax[i] 中的最小值决定。由于数组 leftMax 是从左往右计算，数组 rightMax 是从右往左计算，因此可以使用双指针和两个变量代替两个数组。

维护两个指针 left 和 right，以及两个变量 leftMax 和 rightMax，初始时 left=0,right=n−1,leftMax=0,rightMax=0。指针 left 只会向右移动，指针 right 只会向左移动，在移动指针的过程中维护两个变量 leftMax 和 rightMax 的值。

当两个指针没有相遇时，进行如下操作：

  • 使用 height[left] 和 height[right] 的值更新 leftMax 和 rightMax 的值；
  • 如果 height[left] < height[right]，则必有 leftMax < rightMax，下标 left 处能接的雨水量等于 leftMax − height[left]，将下标 left 处能接的雨水量加到能接的雨水总量，然后将 left 加 1（即向右移动一位）；
  • 如果 height[left] ≥ height[right]，则必有 leftMax ≥ rightMax，下标 right 处能接的雨水量等于 rightMax − height[right]，将下标 right 处能接的雨水量加到能接的雨水总量，然后将 right 减 1（即向左移动一位）。

当两个指针相遇时，即可得到能接的雨水总量。

为什么“如果 height[left] < height[right]，则必有 leftMax < rightMax”？

首先我们要知道，算法的逻辑是“谁小移动谁”，即 height[left] < height[right] 时移动 left，否则移动 right；

假如当前状态是 height[left] < height[right]，

如果 leftMax 很大（比 rightMax 大）：说明我们在左边曾经遇到过一个非常高的柱子（比如高度为 100）。 而在那个时刻（左指针指向 100 时），右边的 rightMax 还很小（比如只有 5）。 根据移动规则：height[left] (100) > height[right] (<=5)。 那时候算法会强迫移动右指针，而左指针会停在那个 100 的位置不动。

左指针什么时候才能动？只有当右指针不断向左移动，并且遇到了一个比 100 还要高的柱子（更新了 rightMax > 100），此时 height[right] > height[left] 了，左指针才会被允许移动。

因此只要左指针在动（说明 height[left] < height[right]），就意味着右边一定已经存在一个比 leftMax 更高的挡板（rightMax）了，否则左指针早就被卡住不动了。

🔧 代码实现

1、动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        if (n == 0) return 0;

        vector<int> leftMax(n);
        vector<int> rightMax(n);

        // 初始化 leftMax
        leftMax[0] = height[0];
        for (int i = 1; i < n; i++) {
            leftMax[i] = max(leftMax[i - 1], height[i]);
        }

        // 初始化 rightMax
        rightMax[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i--) {
            rightMax[i] = max(rightMax[i + 1], height[i]);
        }

        // 计算结果
        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans += min(leftMax[i], rightMax[i]) - height[i];
        }
        return ans;
    }
};

2、单调栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        stack<int> st;
        int n = height.size();
        for(int i = 0; i < n; i++){
            while(!st.empty() && height[st.top()] <= height[i]){
                int top = st.top();
                st.pop();
                if(st.empty()){
                    break;
                }
                int left = st.top();
                ans+= (i - left - 1) * (min(height[left], height[i]) - height[top]);
            }
            st.push(i);
        }
        return ans;
    }
};

3、双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        int ans = 0, left = 0, right = n - 1, leftMax = 0, rightMax = 0;
        while(left < right){
            leftMax = max(height[left], leftMax);
            rightMax = max(height[right], rightMax);
            if (height[left] > height[right]){
                ans+= rightMax - height[right];
                right--;
            } else {
                ans+= leftMax - height[left];
                left++;
            }
        }
        return ans;
    }
};

📊 复杂度分析

1、动态规划

  • 时间复杂度：遍历三次，时间复杂度为 O(N)O(N)。
  • 空间复杂度：需要额外的数组存储leftMax[i],rightMax[i]，空间占用为 O(N)O(N)。

2、单调栈

  • 时间复杂度：遍历一次，时间复杂度为 O(N)O(N)。
  • 空间复杂度：需要额外的数组存储栈，空间占用为 O(N)O(N)。

2、双指针

  • 时间复杂度：遍历一次，时间复杂度为 O(N)O(N)。
  • 空间复杂度：无需额外占用和输入规模相关的存储空间为 O(1)O(1)。

🎯 总结

  • 核心思想：想到朴素算法，一步步优化。